Pergamino de oro
El colega Hilario Moreno del Campo nos hizo llegar su teoría sobre el circuito dorado de Pergamino. Le agradecemos su amable atención y sin más, los invitamos a leerlo.
Recientemente Andy se lanzó, cual Indiana Jones en una de sus aventuras a las que ya nos tiene acostumbrado, a la búsqueda del “comicio dorado”. Y aunque no se animó a teorizar sobre su hallazgo y hasta culpó al azar, su descubrimiento de las “40 mesas de Pergamino” nos dejó pensando a más de uno. Pero vayamos al punto. La cuestión es que se nos ocurrió una hipótesis para explicar estas mesas de oro y, más en general, para plantear algunas conjeturas sobre las condiciones teóricas del “escrutinio dorado” que buscaba Andy. Es decir, decir algo respecto de en qué mesas, circuitos y/o departamentos electorales y bajo qué condiciones, podemos esperar que se reflejen los resultados nacionales con un desvío tolerable. Y alguna justificación de porqué sería lógico esperar esos resultados.
Para el que esté familiarizado con la teoría del muestreo (es decir, que haya estudiado en la facultad metodología con algún interés y haya tenido que profundizar un poco su entendimiento sobre las técnicas de muestreo para una encuesta o cosa parecida) la idea es bastante simple. Para decirlo rápido: los departamentos electorales en los que se puede esperar alta cantidad de “mesas doradas” son los espacialmente medios, que tienden a ubicarse cerca del promedio de una distribución (más o menos tradición peronista, mayor o menor nivel socioeconómico, izquierda o derecha, etc.), y que agrupan a la mayoría de los electores en un circuito único. Nuestra hipótesis es que la ciudad de Pergamino concuerda con estas características y, un poco por eso y otro poco ayudado por el azar que mencionaba Andy, apareció tan fuertemente representado en las 500 mesas que coincidieron con las dos últimas elecciones nacionales.
Para empezar ¿Qué nos diría la teoría de muestreo respecto de la distribución de electores dentro de un circuito? Lo primero que podría decirnos es que las mesas electorales se parecerían mucho a muestras aleatorias (“aleatoria” es la palabra clave) sistemáticas dentro de un circuito. Y que si esto es así, podemos aplicarle a las mesas de un circuito los principios derivados del teorema del límite central o, en castellano, que podemos conocer su margen de error. Dicho con un ejemplo, para una mesa de 350 electores en la que haya 270 votos efectivos, el resultado de una mesa cualquiera y de una lista cualquiera va a coincidir con el promedio del circuito con un desvío menor al 6% (margen de error) en el 95,5% de los casos (nivel de confianza). En términos más generales todavía, la teoría del muestreo nos diría que si un circuito tiene 120 mesas o más, la distribución de los errores de cada mesa respecto a la suma de todas las mesas, va a tener distribución normal, es decir, así:
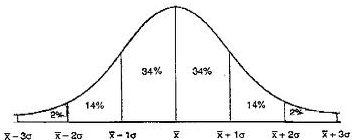
Como se observa en el gráfico, el 34% de las mesas se ubicarían apenas por encima del promedio (a un error estándar) y otro 34% apenas por debajo. Luego otro 14% superior al promedio se ubicaría ya un poco más lejos, lo mismo que otro 14% inferior (fíjense que la suma de estos 4 grupos nos da 95,5%, es decir, el nivel de confianza).
¿Por qué podemos estar seguros que la distribución de mesas dentro de un circuito va a tener esta distribución? Porque dentro de los circuitos el orden que siguen las mesas es alfabético y, en consecuencia, si descartamos que existan diferencias en el voto vinculadas a la letra de inicio de los apellidos, podemos concluir que las mesas se comportan como muestras aleatorias y que las únicas diferencias entre ellas son las que determina el azar o la casualidad (y ya conocemos la distribución de probabilidades que tiene el azar: una curva normal, como en el gráfico de arriba). Lo más probable es, entonces, que cada una de nuestras mesas contengan más o menos la misma heterogeneidad que el circuito en general, es decir, las mismas proporciones (con las variaciones propias del margen de error) de nivel educativo, sexos, edades, color de pelo y hasta preferencias por gustos de helados, entre electores. Y, obviamente, también existirán las mismas altas probabilidades de que estén proporcionalmente representados por mesa los votantes de cada partido político. Esto es básicamente lo que dice la teoría del muestreo y podemos confiar en ello tanto como confiamos en la efectividad de un remedio o en las chances de ganar la lotería, porque todos se basan en los mismos métodos probabilísticos.
Ahora bien, dentro de un departamento (o municipio) los resultados de las mesas no suelen ser tan homogéneos como acabamos de ver. Ello se debe a que, generalmente, el departamento está dividido en circuitos electorales, que al ser territorios contiguos suelen ser homogéneos al interior y distintos entre sí (lo típico es que cada circuito represente a una o más localidades o barrios). Así, cada circuito suele tener ciertas características sociales y eso guarda algún grado de asociación con el voto. Cuando esto ocurre es difícil que cada mesa electoral contenga la heterogeneidad de todo el departamento. En estos casos las mesas estarían diferenciadas, además del azar, por diferencias sociales y demográficas asociadas al sub-territorio local al que pertenece cada una y no serían muestras aleatorias representativas por sí solas de todo el departamento. Sin embargo, en los casos en los que el departamento tiene un gran circuito, las mesas de éste sí suelen contener la heterogeneidad del departamento. En este último caso, la distribución de mesas se asemeja más a una “muestra por conglomerado” (heterogénea al interior y homogénea entre conglomerados) y en el primero a una “muestra estratificada” (homogénea al interior y heterogénea entre estratos).
Respecto de los tipos de circuitos electorales y las “mesas de oro”, digamos entonces que cuando los circuitos son más grandes, las mesas suelen tomar forma de conglomerados de electores (más heterogéneas internamente) y allí es donde es más probable que se den mesas de oro. Pero para que esto ocurra es necesario un segundo requisito: el departamento debe ser un departamento “medio”, es decir, contener en término de electores, un grado de diversidad alto y similar al país en general o, al menos, a su promedio.
Bueno, llegados a este punto podemos decir que nuestra hipótesis es que dentro de las 500 mesas de oro del hackaton 40 resultaron ser de Pergamino porque, además de la probable ayuda del azar, Pergamino sería un departamento con las características mencionadas: tiene (o tuvo en 2007 y 2011) un circuito único en la ciudad de Pergamino, con alrededor de 200 mesas con forma de conglomerados de electores que, además, tendría características heterogéneas y “medias” en términos de ubicación socioespacial nacional (para confirmar esto seriamente, habría que analizar los datos con más detalle que el que tuvimos aquí).
Si nuestras conjeturas son ciertas, es probable que Pergamino no sea el único municipio con estas características y que puedan ser descubiertos otros departamentos que contengan varias mesas de oro. Para ello habría que explorar aquellos que poseen características heterogéneas y medias (ni demasiados ricos ni demasiados pobres, ni muy viejos ni muy jóvenes, ni muy peronista ni muy poco peronista, etc.), que no sean demasiado chicos en cantidad de electores y con circuitos únicos o lo bastante grandes. En realidad, lo que sería dorado no es ni el departamento ni las mesas, sino los circuitos que contienen la suficiente heterogeneidad para ser muestras representativas del país. En esos circuitos, todas las mesas serían potencialmente doradas. Y para predecir tempranamente el resultado de una elección, sólo sería necesario acumular una cantidad suficiente (¿30, 40, 50?) de mesas doradas pertenecientes a distintos circuitos dorados.
Si usted es de Pergamino, puede sentirse orgulloso de que su distrito tenga estas características muestrales tan maravillosas y, quizás, haya colaborado a que los politólogos entendamos un poco más sobre los datos electorales y su distribución. Ah! Y de paso también puede aprovechar y votar a un colega nuestro que se llama Bormioli y se presenta a elecciones en el gran circuito dorado (o perlado mejor dicho, ya que Pergamino es la “Perla del Norte”).
PS: Al cierre de esta nota nos llega el comentario que la Justicia Electoral estaría impulsando la división del «circuito dorado» de Pergamino. Desde ya se trata de otra coincidencia.
Publicado: sábado 7 de septiembre de 2013 a las 8:30 am 
Buenos Aires, Nación. Puede seguir todos los comentarios a esta entrada a través de RSS 2.0.
Puede dejar una respuesta, o referencia desde su propio sitio.
Andy Tow en 
Lautaro en 
Analia en 
Gustavo en 
no estoy muy de acuerdo que sea gaussiano por default en las mesas
sábado 7 de septiembre de 2013 a las 12:55 pmejemplo
una mesa en Recoleta no es lo mismo que una al lado del Hptal Posadas en cuanto a su distribucion etaria, nacionalidad de origen etc etc.
Muy interesante análisis.
lunes 9 de septiembre de 2013 a las 9:51 pmSeria bueno una lista de mesas de oro de todo el pais y el nivel de coincidencia de cada una.
ME pregunto que incidencia futura en las votaciones tendra en una mesa / circuito dorado, saberse circuito dorado?
miércoles 11 de septiembre de 2013 a las 12:13 pm