De Rusia con amor
En una entrada anterior, señalamos al pasar que la distribución de las edades de los dirigentes al asumir y al finalizar el mandato se aproxima una distribución de densidad normal o gaussiana.
Su presencia en las bases arcontológicas de los últimos 250 años sugiere fuertemente que esta forma de la distribución es una regularidad histórica. Es independiente de la forma que adopta en cada momento o lugar la pirámide de la población total y la pirámide de la población ocupada. También se reitera no importa el régimen político. La distribución de las edades se aproxima a la normal tanto en autocracias como en democracias.
La semana pasada, intrigado por esta regularidad, hice lo de siempre: busqué por Google. Entre la madeja usual de información inútil, encontré un resumen de una comunicación presentada al IX Simposio internacional ruso-coreano de ciencia y tecnología sobre regularidades estadísticas en la administración del Estado ruso, de V.V. Gubarev y O. Alsova de la Universidad Técnica Estatal de Novosibirsk.
Como la idea de pagar 29 dólares por leer un artículo académico de 2 páginas no me resultaba muy atractiva, busqué a los autores (otra vez por Google) y les mandé un mail. Casi me había olvidado del asunto cuando hoy recibí por mail el artículo original en ruso. Con la ayuda de un traductor online, pude leerlo (mejor dicho, interpretarlo).
Gubarev y Alsova estudian una población de 104 jefes de Estado rusos desde el año 862 hasta 2004 y advierten que: 1) la distribución de las duraciones de los mandatos se aproxima a la exponencial; 2) la distribución de las edades de los dirigentes al asumir y al finalizar sus mandatos se aproxima a la normal y 3) la correlación entre la edad al asumir y la edad al finalizar el mandato sugiere un modelo de relación lineal1.
Ensayé verificar estas características en bases de datos que compilé: la combinada con Polity IV de más de 7.000 mandatos, la de Rulers completa de más de 13.000 y Archigos, de unos 3.000. La única diferencia metodológica que noté es que ellos incluyeron en el análisis a dirigentes que asumieron siendo menores de edad, mientras que yo excluí a todos los menores de 18 en base al criterio que no ostentaban ejercicio efectivo del cargo.
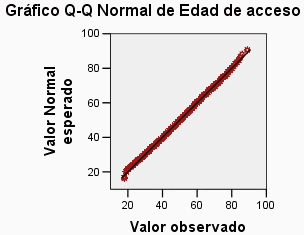Respecto a 1), los gráficos Q-Q de contraste de la distribución de frecuencias de la duración del mandato a la distribución exponencial no muestran ajuste.
Lo contrario se puede decir respecto a 2): los gráficos Q-Q indican que la distribución de la edad de inicio y finalización ajusta a la normal (ver Q-Q a la izquierda).
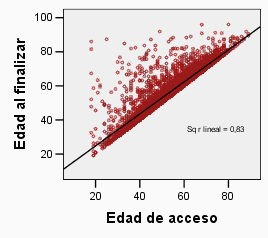
En cuanto a 3), la naturaleza de los datos hace a mi juicio inaplicable el modelo de regresión lineal planteado2.
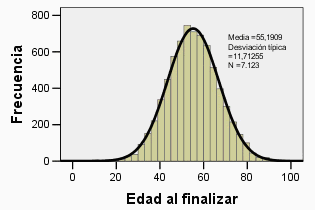
De todas maneras, lo que me interesaba del artículo era que para ellos también la forma de distribución de frecuencias de la edad de los dirigentes al asumir y finalizar sus mandatos se ajustaba a la de densidad normal. De modo que también las edades de los zares rusos desde el siglo IX al asumir y sobre todo al finalizar se distribuyen normalmente.
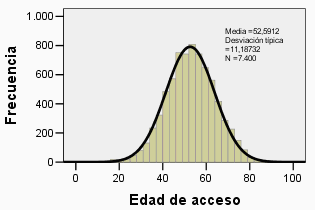¿Qué significa esto? Dejando de lado que a la hora del muestreo no será necesario hacer suposiciones sobre la distribución y varianza de los datos, creo que es un hecho que tiene cierta relevancia. Es difícil pensar en algo menos aleatorio que la determinación de quienes ejercen las más altas magistraturas del Estado. Que las edades de éstos se distribuyan como se distribuyen los errores de medición debe constituir más que una aguda ironía.
La distribución normal describe fenómenos en los que interviene gran número de factores actuando de forma aditiva e independiente. A grandes rasgos, se puede suponer que en la determinación de la edad de los mandatarios confluyen causas biológicas, psicológicas, sociales y políticas. El hecho que la forma de su distribución se mantenga constante en todo tiempo y lugar sugiere que tales causas también se mantienen en gran medida invariables. Al parecer son causas que están fuertemente arraigadas en la sociedad humana.
La edad no solamente denota el paso del tiempo, sino que es una medida resumen de la condición individual en cuanto a conocimiento, experiencia, madurez y lucidez, entre otros atributos. La simetría característica de la distribución normal sugiere un orden, un equilibrio, una suerte de balance del poder distribuido entre un conjunto de individuos cuyas edades los equipan con capacidades diferenciadas.
En Africa, Brasil, Norteamérica y Asia los antropólogos han encontrado sociedades con sistemas formalizados de grupos de edad. Estos grupos a su vez contienen grados de edad dentro de los que los hombres son iniciados para cumplir funciones guerreras y políticas en diferentes etapas de la vida. Este modo de organización es parte integral del sistema social y su remoción significaría el colapso del orden social y político3.
¿Es la distribución etaria gaussiana el reflejo de un orden implícito? Llegados a este punto, estimamos prudente descansar. La sombra de Quetelet se proyecta en el tópico menos pensado.
- Статистические Закономерноости Правления Российским Государством, KORUS 2005. [↩]
- La distribución de los residuales dista de ser aleatoria habiendo una asíntota entre las variables: la edad al finalizar nunca puede ser menor a la edad al asumir y viceversa. Es posible que los rusos no se hayan percatado de esta violación del supuesto de distribución normal del error debido a que la asíntota en el gráfico de dispersión de una población más pequeña no resulta tan notoria.
[↩] - Encyclopaedia Britannica, vol. I, 1963, p.325 [↩]
Publicado: viernes 30 de mayo de 2008 a las 10:13 pm 
Mundo. Puede seguir todos los comentarios a esta entrada a través de RSS 2.0.
Puede dejar una respuesta, o referencia desde su propio sitio.
Comentarios recientes